[알고리즘] N-퀸

08 Jul 2025 in Study / Coding Test

• ☑️ 문제
• ☑️ 풀이

☑️ 문제

가로, 세로 길이가 n인 정사각형 체스판이 있다. 체스판 위의 n개의 퀸이 서로를 공격할 수 없도록 배치하고 싶다. 체스판의 길이 n이 주어질 때 조건을 만족하는 퀸 배치 수를 반환하는 함수를 완성하라.

☑️ 풀이

public class Solution46 {

    private static int N; 
    private static boolean[] width; 
    private static boolean[] diagonal1; 
    private static boolean[] diagonal2; 

    private static int getAns(int y) {
        int ans = 0;

				// 1. 
        if (y == N) {
            ans++;
        }
        else {
			       // 2.
            for (int i = 0; i < N; i++) {
		            // 3. 
                if (width[i] || diagonal1[i + y] || diagonal2[i - y + N]) {
                    continue;
                }
								// 4. 
                width[i] = diagonal1[i + y] = diagonal2[i - y + N] = true;

								// 5.
                ans += getAns(y + 1);
								
								// 6. 
                width[i] = diagonal1[i + y] = diagonal2[i - y + N] = false;
            }
        }

        return ans;
    }

    public static int solution(int n) {
        N = n;
        width = new boolean[n];
        diagonal1 = new boolean[n * 2];
        diagonal2 = new boolean[n * 2];

        int answer = getAns(0);
        return answer;
    }
}

• getAns() : 퀸이 서로 공격할 수 없도록 배치하는 경우의 수를 구하는 메서드
  • N : 체스판의 크기
  • y : 현재 퀸을 놓을 위치 (행)
  • width[i] : 특정 열에 퀸이 위치했는지 표시
  • diagonal1 : 오른쪽 위 → 왼쪽 아래로 대각선 방향에서 퀸 중복 체크용 배열
    diagonal2 : 왼쪽 위 → 오른쪽 아래로 대각선 방향에서 퀸 중복 체크용 배열

    • diagonal1과 diagonal2는 체스판의 행과 열의 합을 이용하여 대각선을 체크하는 배열이다.

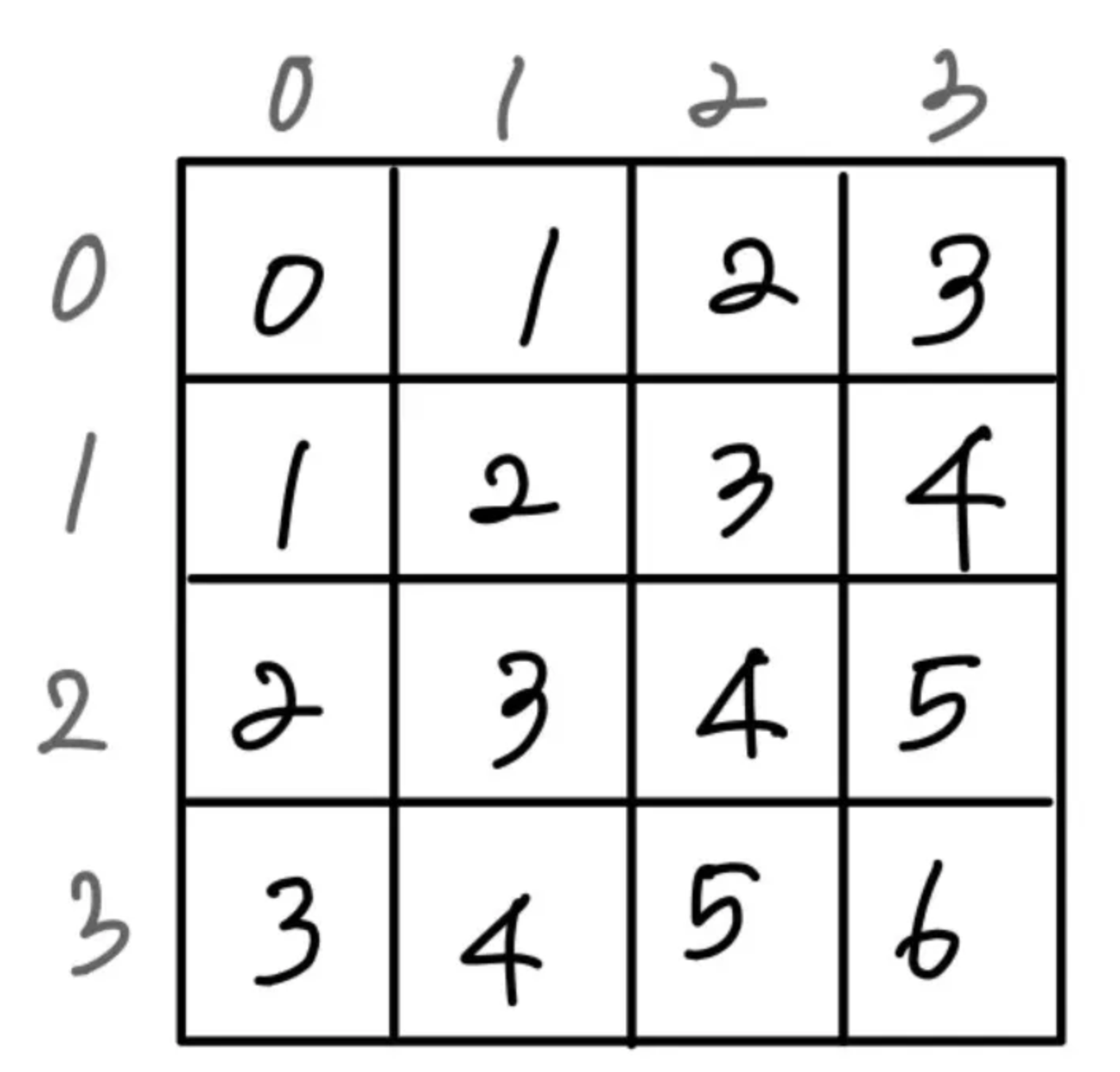
    • (0,0), (3,1)에 퀸이 놓여있는 상태라면, diagonal1[0]과 diagonal[4]는 true이다.
      이 때, (2,2)와 (3,1)에 퀸을 놓으려 하면 diagonal1[0]과 diagonal[4]가 true이기 때문에 대각선상에 퀸이 있음을 알 수 있다.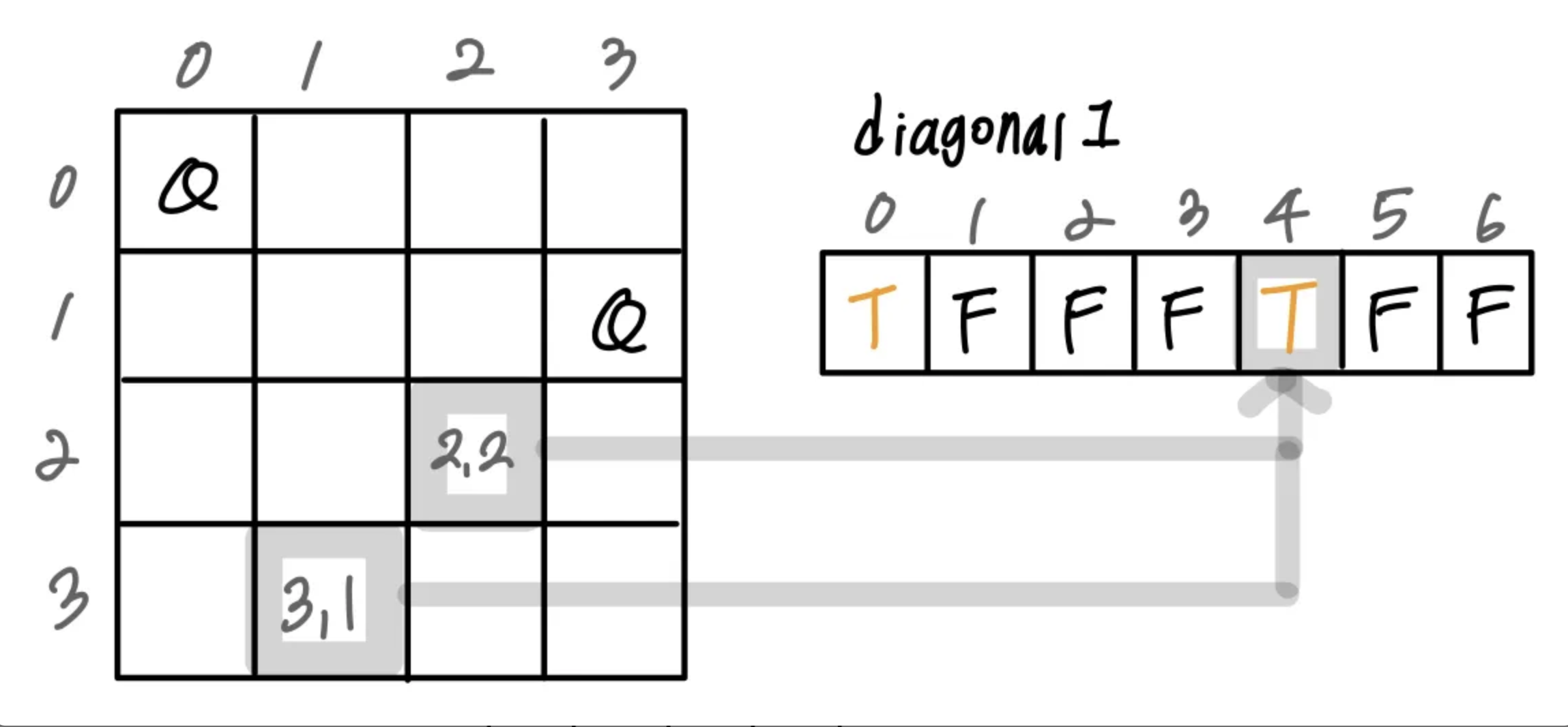

• 로직 설명
  1. y == N 이면 모든 퀸의 위치가 결정된 경우이다.
     1. y는 현재 행 번호이자 현재 위치가 결정된 퀸의 개수를 의미한다.
     2. 퀸을 놓는 규칙에 맞지 않으면 더 이상 탐색하지 않으므로 백트래킹한다.
     3. 퀸을 놓는 규칙에 맞으면 ans + 1하고 그렇지 않으면 계속 탐색한다.
  2. 현재 행에서 퀸이 놓일 수 있는 모든 위치를 시도한다.
  3. 만약 해당 열(width)에 퀸이 있거나, 대각선(diagonal1, 2)에 퀸이 있다면 스킵한다.
  4. 그렇지 않다면, 퀸을 놓아 width, diagonal1, 2를 갱신한다.
  5. 다음 행으로 이동(y+1)하여 재귀를 계속 진행한다.
  6. 백트래킹 진행을 위해 해당 열에 퀸을 놓았을 때 탐색이 완료되면 다시 false로 바꿔 퀸을 제거한다.
• 시간복잡도
  • N은 퀸의 개수
  • 각 행에 퀸을 놓는 방법의 경우의 수는 N * (N-1) * … * 1 → O(N!)
  • 실제 연산은 유망 함수에 의해 훨씬 적음